여러분은 모두 '빛의 속도'로 움직이고 있습니다

제목 내용을 말씀드리기 전,
몇가지 예시에서 ‘기준’에 관련된 이야기를 하려고 합니다. 본업(?)에 집중해야하는데,
시험기간엔 린스 뒤쪽 설명 구경도 재밋듯이 계속 다른 재밋는게 생각나서 급하게 준비해서 합니다

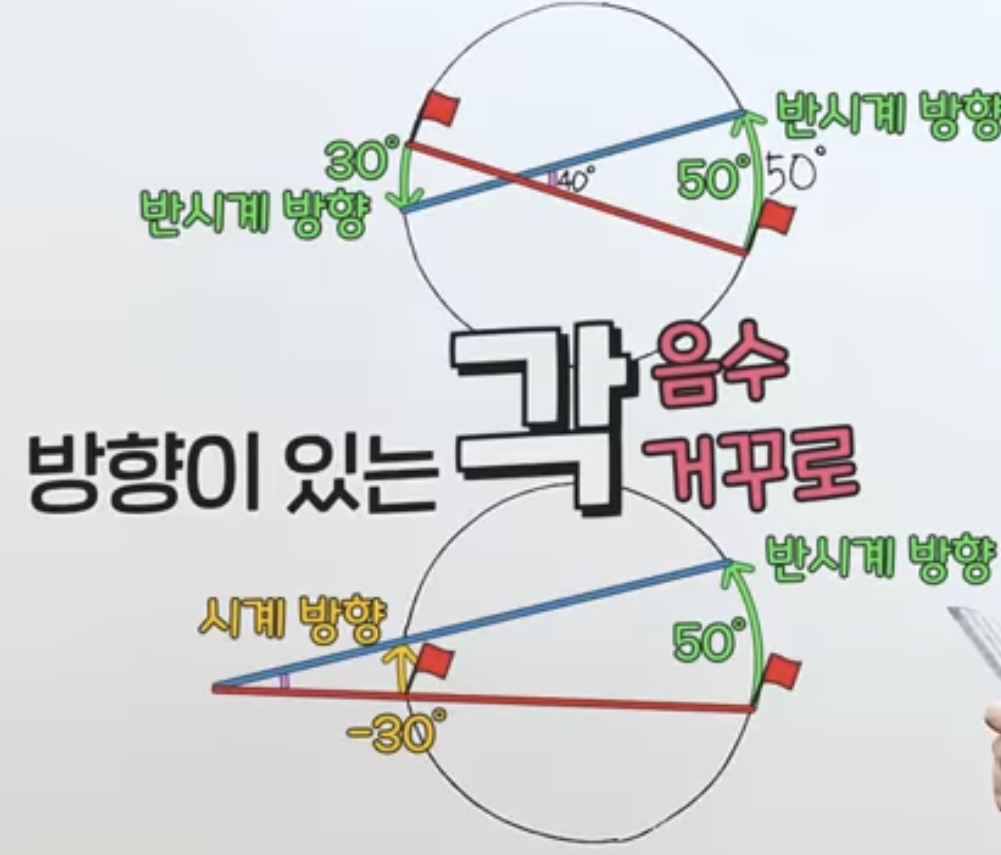
[도형 각 구하기]

풀이

그럼 요건?

풀이

요약.

 

여기서 기준에 대한 이야기 

기준을 어느곳으로 두느냐에 따라 풀이도 바뀌고, 일관된 규칙으로 답을 설명 할 수 있다.

 

[기저 이야기]
3D 회전 스터디 내용에서 잠시 언급됐었지만 '기저'라는 개념이 있습니다.
(기저는 좌표계에서의 기준이라고 생각하시면 면 됩니다. 정확한 정의는 선형대수학에서 벡터공간을 선형생성하는 선형독립인 벡터집합)
회전 행렬을 곱한 기저벡터 자체를 먼저 계산해놓아서 매픽셀마다 회전행렬을 곱하지 않아도 되게 하는 최적화였죠.

 

여기서는 기준자체를 바꿔서 원하는 목적(회전)을 달성 합니다.

[동차좌표계 이야기]
DX에서도 나온 내용인데, 아시는분이 갑자기 연락오셔서 질문하신..
사영기하학이라는 학문이 있습니다.

이득우아저씨 블로그 2가지
https://m.blog.naver.com/destiny9720/221424260572

https://m.blog.naver.com/PostView.naver?blogId=destiny9720&logNo=221424362110&targetKeyword=&targetRecommendationCode=1

28. 동차 좌표계(Homogeneous Coordinate System)

그럼 이 동차 좌표계를 렌더링 파이프라인에서 왜 쓸까? 아니 정확히 궁금했던건 누구 때문에 w하나를 추가하나?
위치변환(translation)과 투영변환(projection)이 단순 선형변환이 아니기 때문에 3x3 행렬로 표현할 수 없는데, 이러면 렌더링 파이프라인이 복잡해지니, 얘네들의 변환을 행렬로 표현하기 위해 사용한다. 사실 책에서 변환 부분 설명할 때 행렬의 모양을 잘 보면 이 두 변환 외에는 w값을 건드리는 경우가 없다. (뷰 행렬도 건드리지만 이건 카메라 위치 변환 때문이니 넘어가자)

지인분께서 질문하신 내용은 사영기하학에서의 정육면체와 유클리드기하학에서의 정육면제는 같은 모양으로 보이나? 였는데, 여러분들 생각은 어떤가요?


여기서 유클리드 기하학은 무한대라는 개념이 없습니다. 평행한 두 직선은 영원히 만나지 않습니다.
하지만 사영기하학은 다르죠. 소실점이라는 무한대의 개념이 있습니다.

그래서 사영기하학의 제 2공리는 '평면위의 두 직선은 최소한 한 점 위에서 만난다' 입니다.

사용하는 좌표'계' 즉, System이 다르기때문에 두 기하학에서의 모양은 다르게 보일 수 밖에 없습니다.

애초에 우리「눈」에 맞춰서 설계된게 사영기하학이니까요.

반대로 유클리드 기하학은 우리 「머리」속의 완전무결한 기하학입니다

 

System은 해당 차원에 적용되는 공통 "기준"입니다.

 

[중력가속도가 왜 파이제곱인지]
시간이 어떻게 정해졌는지 생각해봐야합니다.

https://blog.naver.com/a4gkyum/220778576131

중력가속도가 파이의 제곱인 이유

<중력가속도란?>

결론부터 얘기해봅시다.
중력가속도는 낙하하는 물체에 붙는 가속도입니다.

어떤 물체를 떨어트린다고 해봅시다. (뜬금포상식: '떨어트리다'와 '떨어뜨리다'는 둘다 표준어)
아마 경험상 물체가 떨어지면 떨어질수록 점점 속력이 빨라진다는 것을 아실 겁니다.

이는 물체에 중력이라는 힘이 작용하기 때문입니다.
그리고 뉴턴의 제2법칙(모른다면 클릭)에 따라 힘이 작용하는 물체에는 가속도가 붙죠.
이 가속도가 바로 중력가속도입니다.
따라서 떨어지는 물체의 속력이 점점 빨라지는 겁니다.

여기서 잠깐 만유인력이란 것을 짚고 넘어갑시다.

모든 물체는 서로를 끌어당기는 상호작용을 합니다. 마치 자석처럼요.
그러니까 굳이 자석이 아니더라도 두 물체를 가까이 놓으면 두 물체 사이에는 서로를 끄는 힘이 작용합니다. 단지 그 힘이 너무너무 작아서 우리가 느끼질 못하죠.

이 힘을 바로 만유인력이라고 합니다.
만유인력은 두 물체 사이의 거리가 가까울수록, 두 물체의 질량이 클수록 커집니다.
지구는 질량이 매우매우 크기 때문에(적어도 저희랑 비교했을 때) 만유인력이 꽤나 강하게 작용해 저희를 끌어당기죠. 이것이 바로 중력입니다.

만유인력 공식은 다음과 같습니다.

여기서 G는 만유인력 상수(6.6726×10-11m3/kg2), M과 m은 두 물체의 질량, r은 두 물체 사이의 거리입니다.

근데 이 만유인력 식이 왠지 뉴턴의 제2법칙을 닮았습니다.

그렇다면 만유인력 식의 형태를 F=ma 로 바꿔보겠습니다.

어때요? 뉴턴의 제2법칙과 형태가 똑같죠?
여기서 r=(지구 반지름), M=(지구 질량), G=(만유인력 상수)를 대입한 값이
지구에서의 중력가속도로, 약 9.8m/s² 입니다. 즉, 말이 길었는데 한마디로 요약하자면
중력가속도란 지구에서 낙하하는 물체가 중력을 받음으로써 인해 가지게 되는 가속도입니다.
그리고 이 중력가속도는 낙하하는 현상이나 물체,
아니면 굳이 낙하가 아니더라도 진자, 포물선 운동, 궤도 운동 등 중력이 관여하는 모든 운동에는 중력가속도가 나타납니다.

<초진자로 정해진 1m>

이 파이의 제곱이 중력가속도이다 얘기를 하려면
역사적으로 좀 거슬러 올라가야 합니다.
그것도 기원전으로요;;;

1초는 어떻게 정의되었을까요?

아마 60진법을 사용하던 메소포타미아인들이 해가 하늘에서 똑같은 위치에 걸리기까지 걸리는 시간, 1년을 12달로 나누고, 한 달을 30일로 나누고, 하루를 24시간으로 나누고, 한시간을 60분으로 나누고, 1분을 60초로 나눠서 1초를 정의했을 것입니다.

이런 정의는 1900년대까지 이어져 내려오다가, 지구의 자전 속도가 일정하지 않다는 사실을 깨닫고 1967년 절대적이고 엄밀한 1초의 정의 기준을 찾던 중
세슘 원자의 초미세 전이가 완벽히 규칙적임을 알아내 이로 1초를 새로 정의했습니다.
(현재의 1초의 정의: 그리고 바닥 상태에 있는 두 개의 초미세 에너지 준위 사이의 전이진동에서 방출되는 복사선이 9,192,631,770억번 진동하는 시간)


그러면 1m는 어떻게 정의되었을까요?

사실 1m의 역사는 1초만큼 오래되지 않았습니다.
거의 모든 문화에서 사람의 발 크기, 손 크기 등 이런 신체부위를 단위로 삼아 길이를 측량했죠.
하지만 단연 신체부위는 사람마다 다르기 일쑤.
따라서 엄밀하고 통일된 단위가 필요하다는 인식이 1600년대 중반에야 나타났습니다.

과학에 아주 관심있는 사람이면 알겠지만
갈릴레오는 1582년에 진자의 등시성을 발견했습니다. (알겠습니다. 아무리 과학에 미쳐있더라 해도 갈릴레오가 진자의 등시성을 발견한 년도까지는 모르겠네요)

진자의 등시성이란, 진자의 주기는, 즉 한번 왕복하는데 걸리는 시간은 추의 무게와는 상관없이 실의 길이에만 상관있다는 법칙입니다.

과학자들은 이런 진자의 등시성과 1초가 이미 정의되어있다는 점으로부터 새로운 단위를 정하려고 했습니다. 즉, 한 쪽 끝에서 다른 쪽 끝으로 가는데 걸리는 시간이 1초인 진자의 실의 길이를 1m라는 새로운 단위로 정의하자는 생각이었죠.
이런 진자, 즉, 주기가 2초(한 쪽 끝에서 다른 쪽 끝으로 가는데 걸리는 시간이 1초이므로 왕복하는데 걸리는 시간은 2초)인 진자를 초진자라고 합니다. (여러분들에게는 괘종시계로 더 익숙하죠)

이렇게 초진자의 실의 길이를 1m로 정하자는 움직임이 한창이었으나
결국은 지구의 크기를 어떤 수로 나누어서 1m를 정의하자는 채택안이 결의되었고,
지구의 크기를 최대한 초진자의 실의 길이에 맞도록 나누어서 현재의 1m가 정의되었습니다.
(현재의 1m의 정의: 빛이 1초에 가는 거리를 299,792,458로 나눈 거리)

이렇게 해서 초진자의 실의 길이는 0.994m로, 약 1m가 되었습니다.


<진자와 파이>

일정한 주기를 가지고 직선 상에서 왔다갔다 하는 운동을 단진동이라고 합니다.
대표적인 단진동 운동은 용수철에 매달린 물체의 운동이죠.
왔다 갔다 하잖아요?

우리가 일반적으로 생각하는, 천장에 줄을 고정하고 거기에 추를 매다는 진자를 단진자라고 합니다.

그런데 단진자를 아주 살짝 들었다가 놓았다고 합시다.

그럼 그 단진자는 거의 직선에 가까운 운동을 하겠죠.
그렇다면 직선 상에서 왔다 갔다 하는 운동이므로, 이 역시 단진동입니다.

그런데 등속 원운동의 그림자 역시 단진동입니다.

따라서 단진자와 등속 원운동의 물리적 성질이 비슷할 거라는 추론이 가능하죠.

등속 원운동의 주기는 당연히 π로 이루어진 식입니다. (T=2π/ω)
이로부터 단진자의 주기를 구하면, 다음과 같은 식이 나옵니다.

여기서 T는 진자의 주기, L은 진자의 실의 길이, g는 중력가속도입니다.
그럼 이 식을 초진자에 대입해 봅시다.

초진자의 주기는 2초, 실의 길이는 약 1m이므로,
값을 대입하고 식을 정리해보면

따라서

이므로 파이의 제곱이 중력가속도임을 확인할 수 있었습니다.
크~ 근데 뭔가 아쉽네요.
만약 초진자의 실의 길이를 정확히 1m로 정의했다면 파이의 제곱이 정확히 중력가속도인,
그런 물리상수와 수학상수의 환상적인 조합을 이뤄낼 수 있었을 텐데 말이지요..ㅎㅎ

 

한줄 요약: 중력가속도와 파이는 진자의 주기를 구하는 식에서 같이 나타나는데, 초진자의 실의 길이가 1m임에 따라 중력가속도는 파이의 제곱이다.

 

 

[상대성이론 이야기]
↑진짜 수박 겉핡기 수준이라는점을 강조. 특히 일반상대성이론을 제대로하려면 대학원 수준의 수학지식이 있어야함. (대수위상수학, 미분기하/위상수학 필수) 특수상대성이론도 민코프스키 다이어그램, 시공간의 기하학적 해석 등등

(사실 이 내용 알려드리고 싶어서 스터디 한다고 함)
이렇게 충격적이고 직관적으로 알려주는 영상이 없었던것 같아서..

맥스웰 방적식에서 시작되는데..

특수 상대성 이론의 결론은 다음과 같이 대략 요약할 수 있다.

1. 관측자에 대해 빠른 속도로 운동하는 물체는 시간이 느려진다 (시간 지연).
2. 관측자에 대해 빠른 속도로 운동하는 물체는 고전적 운동량보다 더 큰 값을 가진다.
3. 관측자에 대해 빠른 속도로 운동하는 물체는 길이가 짧아진다.
4. 질량이 에너지로, 혹은 에너지가 질량으로 바뀔 수 있다.(E=mc^2 / E=mc2)

일반 상대성 이론의 결론은

1. 중력과 가속도는 구별할 수 없는, 본질적으로 같은 것이다. 비유를 들어 설명하면, 우리가 지금 지구에 서있는 것과 무중력 상태에서 9.8m/s로 윗방향으로 가속되는 엘리베이터에 타고 있는 것은 완전히 같다는 뜻.
2. 강한 중력은 시공간을 휘게 한다. (블랙홀의 경우 시공간에 구멍을 뚫는다고 생각해도 된다.)
3. 정지한 쪽의 시간이 더 길게 간다.

모든 것은 시공간에서 빛의 속도로 움직이고 있고,
질량이 사라지는것은 시공간평면에서 멈추는 것.

 

상대성이론은 빛의 속도가 최고 속도라는 "기준"을 잘 잡아서 나온 이론.

 

이를 잘 설명한 영상이 있는데.
https://youtu.be/vLo1SP_ndpw

 

위 내용을 기반으로 생각해보면
1600km/h로 지구 자전
110,000km/h로 태양 주위를 돌고있음
태양은 880,000km/h로 은하를 돌고있음
은하는 수백만km/h로 우주에서 이동중

우주에서 정지되어 있는것은 하나도 없고 모두가 움직이고 있고 모두가 빛의 속도를 가진다.
우주는 팽창하고 있기때문에 그만큼 시간이 생성되고 있다. (시간은 공간이기 때문에)

E=mc^2
https://youtu.be/AjmZMsxAgrY

병주고 약줌
(특수상대성이론으로 시간여행은 불가능하다. 해놓고 일반상대성이론으로 그래도 혹시 가능할 수도 있지 않을까? 라고..) 그래서 인터스텔라에서..

맥스웰 방적식으로부터 상대성이론, 이후 양자역학까지..
끈이론, M이론, 양자중력학 (현실주의 양자역학), 통일장이론
에테르, 타키온 같은 실존하는지 모르는 애들도 있는데.. 이건 따로..

[쌍둥이 역설]
이제 상대성이론이 어떤건지 대충 알게 됐다고 치고.. 이런 역설도 있다!
https://surpriser.tistory.com/775?category=880713

쌍둥이 역설(Twin Paradox)

[결론 : 기준에 관한 기준]
인간이 세운 기준은 불완전하고 (인식자체가 불완전하기 때문) 그때그때 맞춰서 정해지지만
기준을 잘 잡는게 문제 해결에 큰 도움이 된다.

반대로 기준을 잘 못잡으면 문제는 (제자리걸음 이상) 더 어려워진다.

 

절대적인 기준은 잘 없지만 있다면 따르는게 이후까지 생각하면 이롭다.
그리고 보통 많이 쓰는 기준이 절대적인 기준에 가까울 확률이 높다. ex디자인패턴 (절대적이라는게 아니다!)

결론을 말씀드리면, 기준을 잘 잡으세요.
그리고 기준을 끊임없이 의심하세요. 거기에서 새롭고 좋은 아이디어가 시작됩니다.